常见排序算法分类
十种常见排序算法一般分为以下两种:
(1) 非线性时间比较类排序:
- 交换类排序(快速排序和冒泡排序)
- 插入类排序(简单插入排序和希尔排序)
- 选择类排序(简单选择排序和堆排序)
- 归并排序(通常为二路归并)
(2) 线性时间非比较类排序:计数排序、基数排序和桶排序。
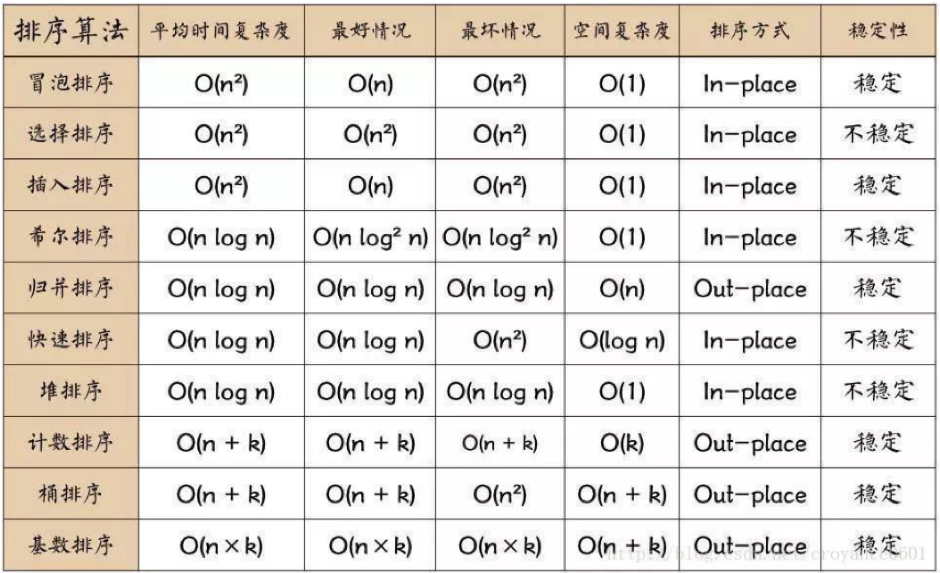
总结:
(1)在比较类排序中,归并排序号称最快,其次是快速排序和堆排序,两者不相伯仲,但是有一点需要注意,数据初始排序状态对堆排序不会产生太大的影响,而快速排序却恰恰相反。
(2)线性时间非比较类排序一般要优于非线性时间比较类排序,但前者对待排序元素的要求较为严格,比如计数排序要求待排序数的最大值不能太大,桶排序要求元素按照hash分桶后桶内元素的数量要均匀。线性时间非比较类排序的典型特点是以空间换时间。
交换类排序
交换排序的基本方法是:两两比较待排序记录的排序码,交换不满足顺序要求的偶对,直到全部满足位置。常见的冒泡排序和快速排序就属于交换类排序。
冒泡排序
特点:稳定排序(stable sort)、原地排序(In-place sort)
最坏运行时间:O(n^2)
最佳运行时间:O(n^2)(如果待排序数据序列为正序,则一趟冒泡就可完成排序)
原理:两层循环,里循环从未排序的数中两两相邻比较并交换,比较每一轮里循环下来找出剩余未排序数的中的最大(小)数并”冒泡”至数列的顶端。
快速排序
特性:不稳定排序(unstable sort)、原地排序(In-place sort)。
最坏运行时间:O(n^2) 每趟排序结束后,元素全部属于某一边子文件,例如原本有序的序列。解决办法是使用快排前先shuffle序列。
最佳运行时间:O(nlgn) 每趟排序结束后,每次划分使两个子文件的长度大致相等
原理:
(1)从待排序的n个记录中任意选取一个记录(通常选取第一个记录)为分区标准;
(2)把所有小于该排序列的记录移动到左边,把所有大于该排序码的记录移动到右边,中间放所选记录,称之为第一趟排序;
(3)然后对前后两个子序列分别重复上述过程,直到所有记录都排好序。
快排代码一例:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24public static void quickSort(int[] arr){
quickSort(arr, 0, arr.length-1);
}
private static void quickSort(int[] arr, int low, int high){
if (low < high){
int pivot=partition(arr, low, high); //将数组分为两部分
quickSort(arr, low, pivot-1); //递归排序左子数组
quickSort(arr, pivot+1, high); //递归排序右子数组
}
}
private static int partition(int[] arr, int low, int high){
int pivot = arr[low]; //枢轴记录
while (low<high){
while (low<high && arr[high]>=pivot) --high;
arr[low]=arr[high]; //交换比枢轴小的记录到左端
while (low<high && arr[low]<=pivot) ++low;
arr[high] = arr[low]; //交换比枢轴小的记录到右端
}
//扫描完成,枢轴到位
arr[low] = pivot;
//返回的是枢轴的位置
return low;
}
插入类排序
插入排序的基本方法是:每步将一个待排序的记录,按其排序码大小,插到前面已经排序的文件中的适当位置,直到全部插入完为止。
直接插入排序
特点:稳定排序(stable sort)、原地排序(In-place sort)。插入排序比较适合用于“少量元素的数组”。
最优复杂度:当输入数组就是排好序的时候,复杂度为O(n),而快速排序在这种情况下会产生O(n^2)的复杂度。
最差复杂度:当输入数组为倒序时,复杂度为O(n^2)
原理:两层循环,每一轮里循环将一个元素插入到前面已经有序的元素中
希尔排序
特点:不稳定排序(stable sort)、原地排序(In-place sort)。
时间复杂度:希尔算法的性能与所选取的增量(分组长度)序列有很大关系。只对特定的待排序记录序列,可以准确地估算比较次数和移动次数。想要弄清比较次数和记录移动次数与增量选择之间的关系,并给出完整的数学分析,至今仍然是数学难题。
原理:
Shell排序法是对相邻指定距离(称为增量)的元素进行比较,并不断把增量缩小至1,完成排序。
Shell排序开始时增量较大,分组较多,每组的记录数目较少,故在各组内采用直接插入排序较快,后来增量逐渐缩小,分组数减少,各组的记录数增多,但由于已经按分组排序,文件叫接近于有序状态,所以新的一趟排序过程较快。因此Shell排序在效率上比直接插入排序有较大的改进。
在直接插入排序的基础上,将直接插入排序中的1全部改变成增量d即可,因为Shell排序最后一轮的增量d就为1。
增量选择:比较常用的是每次取半, Knuth增量序列 h1=1,hi=3∗hi-1+1, Hibbard增量序列 h1=1,hi=2∗hi-1+1
希尔排序一例:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21public static int[] ShellSort(int[] arr){
if(arr == null || arr.length <= 1){
return arr;
}
//希尔排序 升序
for (int d = arr.length / 2; d > 0; d /= 2){ //d:增量 7 3 1
for (int i = d; i < arr.length; i++){
//i:代表即将插入的元素角标,作为每一组比较数据的最后一个元素角标
//j:代表与i同一组的数组元素角标
for (int j = i-d; j>=0; j-=d){ //在此处-d 为了避免下面数组角标越界
if (arr[j] > arr[j + d]) {// j+d 代表即将插入的元素所在的角标
//符合条件,插入元素(交换位置)
int temp = arr[j];
arr[j] = arr[j + d];
arr[j + d] = temp;
}
}
}
}
return arr;
}
选择类排序
选择类排序的基本方法是:每步从待排序记录中选出排序码最小(大)的记录,顺序放在已排序的记录序列的后面,直到全部排完。
简单选择排序
特性:原地排序(In-place sort),不稳定排序(unstable sort)。
思想:每次找一个最小值。
最好情况时间:O(n^2)。
最坏情况时间:O(n^2)。
原理:从所有记录中选出最小的一个数据元素与第一个位置的记录交换;然后在剩下的记录当中再找最小的与第二个位置的记录交换,循环到只剩下最后一个数据元素为止。
堆排序
特性:不稳定排序(unstable sort)、原地排序(In-place sort)。
最优时间:O(nlgn)
最差时间:O(nlgn)
原理:堆排序利用了大根堆(或小根堆)堆顶记录的关键字最大(或最小)这一特征,使得在当前无序区中选取最大(或最小)关键字的记录变得简单。
复合排序
二路归并排序
特点:稳定排序(stable sort)、Out-place sort
思想:运用分治法思想解决排序问题。
最坏情况运行时间:O(nlgn)
最佳运行时间:O(nlgn)
原理:
(1)申请空间,使其大小为两个已经排序序列之和,该空间用来存放合并后的序列
(2)设定两个指针,最初位置分别为两个已经排序序列的起始位置
(3)比较两个指针所指向的元素,选择相对小的元素放入到合并空间,并移动指针到下一位置
(4)重复步骤3直到某一指针达到序列尾
(5)将另一序列剩下的所有元素直接复制到合并序列尾
(6)在此之前将子序列递归归并。子序列元素数量较少时可采用其他排序方法。
桶排序
特性:out-place sort、stable sort。
最坏情况运行时间:当分布不均匀时,全部元素都分到一个桶中,则O(n^2)
最好情况运行时间:O(n)
思想:
桶排序的基本思想是将一个数据表分割成许多buckets,然后每个bucket各自排序,或用不同的排序算法,或者递归的使用bucket sort算法。也是典型的divide-and-conquer分而治之的策略。
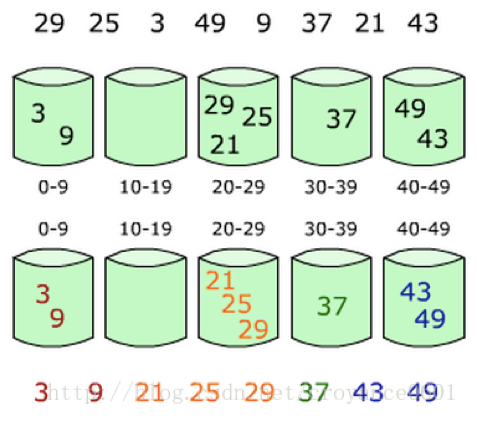
线性时间非比较类排序
计数排序
计数排序是一个非基于比较的排序算法, 它的优势在于在对于较小范围内的整数排序。它的复杂度为Ο(n+k),快于任何比较排序算法,缺点就是非常消耗空间。很明显,如果而且当O(k)>O(n*log(n))的时候其效率反而不如基于比较的排序,比如堆排序和归并排序和快速排序。
k为待排序列所在区间中独立元素的个数。举例来说,若带排序列为[5,3,1,0,2],其所在区间为[0,5],其中独立元素有0,1,2,3,4, k=5
特性:stable sort、out-place sort。
最坏情况运行时间:O(n+k)
最好情况运行时间:O(n+k)
空间复杂度:Ο(k)。
原理: 基本思想是对于给定的输入序列中的每一个元素x,确定该序列中值小于x的元素的个数。一旦有了这个信息,就可以将x直接存放到最终的输出序列的正确位置上。例如,如果输入序列中只有17个元素的值小于x的值,则x可以直接存放在输出序列的第18个位置上。当然,如果有多个元素具有相同的值时,我们不能将这些元素放在输出序列的同一个位置上,在代码中作适当的修改即可。
实现:
(1)根据k构造count序列,用于存放待排序列source中元素数量的统计。
(2)根据source构造result序列,用于存放排好序的元素
(3)统计source中各元素数量,存入count
(4)修改count,使其统计数量依次叠加
(5)遍历source,根据count中的信息填充result
计数排序一例:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20public int[] countSort(int[] source, int k, int min){
int[] count = new int[k]; //构建count数组用于统计各元素个数
int[] result = new int[source.length]; //result数组用于存放最终结果
for (int i=0; i<source.length; i++ ) {
//source中值为min的数量保存在count[0], 值为min+1的数量保存在count[1],以此类推
count[source[i]-min]++;
}
//修改count使其变成计数和累加形式
int sum = 0;
for (int i=0; i<count.length; i++) {
sum += count[i];
count[i] = sum;
}
//遍历source,根据count中的信息填充result
for (int i=0; i<source.length; i++ ) {
result[count[i]-1] = source[i];
}
return result;
}
基数排序
基数排序(以整形为例),将整形10进制按每位拆分,然后从低位到高位依次比较各个位。主要分为两个过程:
(1)分配,先从个位开始,根据位值(0-9)分别放到0~9号桶中(比如64,个位为4,则放入4号桶中);
(2)收集,再将放置在0~9号桶中的数据按顺序放到数组中;
重复(1)(2)过程,从个位到最高位(比如32位无符号整形最大数4294967296,最高位为第10位)。基数排序的方式可以采用LSD(Least significant digital)或MSD(Most significant digital),LSD的排序方式由键值的最右边开始,而MSD则相反,由键值的最左边开始。
以【520 350 72 383 15 442 352 86 158 352】序列为例,排序过程描述如下:
平均时间复杂度:O(dn)(d为基数,此例即表示整形的最高位数)。
空间复杂度:O(10n) (10表示0~9,用于存储临时的序列) 。
稳定性:稳定。