图的基本概念
(1)图是由顶点集合以及顶点间的关系集合组成的一种数据结构。
Graph = (V,E) V是顶点的又穷非空集合;E是顶点之间关系的有穷集合,也叫边集合。
(2)无向图
若顶点Vi到Vj之间的边没有方向,则称这条边为无向边,用无序偶对(Vi,Vj)来表示。如果图中任意两个顶点时间的边都是无向边,则称该图为无向图: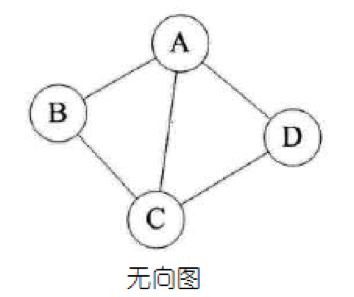
由于是无向图,所以连接顶点A与D的边,可以表示为无序对(A,D),也可以写成(D,A)
对于如上无向图来说,G=(V,{E}) 其中顶点集合V={A,B,C,D};边集合E={(A,B),(B,C),(C,D),(D,A),(A,C)}
(3)有向图
有向边:若从顶点Vi到Vj的边有方向,则称这条边为有向边,也称为弧。
用有序偶<Vi,Vj>来表示,Vi称为弧尾,Vj称为弧头。
如果图中任意两个顶点之间的边都是有向边,则称该图为有向图: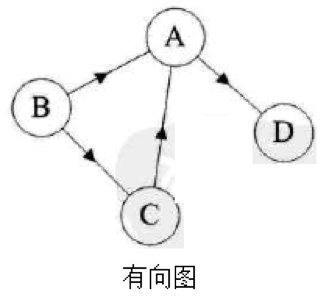
连接顶点A到D的有向边就是弧,A是弧尾,D是弧头,<A,D>表示弧。注意不能写成<D,A>。
对于如上有向图来说,G=(V,{E})其中顶点集合V={A,B,C,D};弧集合E={<A,D>,<B,A>,<C,A>,<B,C>}
(4)完全图
完全无向图:若有n个顶点的无向图有n(n-1)/2 条边, 则此图为完全无向图。
完全有向图:有n个顶点的有向图有n(n-1)条边, 则此图为完全有向图。
(5)树中根节点到任意节点的路径是唯一的,但是图中顶点与顶点之间的路径却不是唯一的。
路径的长度是路径上的边或弧的数目。
(6)如果对于图中任意两个顶点都是连通的,则成G是连通图。
(7)图按照边或弧的多少分稀疏图和稠密图。 如果任意两个顶点之间都存在边叫完全图,有向的叫有向图。
若无重复的边或顶点到自身的边则叫简单图。
(8)图中顶点之间有邻接点。无向图顶点的边数叫做度。有向图顶点分为入度和出度。
(9)图上的边和弧上带权则称为网。
(10)有向的连通图称为强连通图。
图的存储结构
关于图的存储结构,可以分为以下五种:
邻接矩阵
图的邻接矩阵存储方式是用两个数组来表示图:
一个一维数组存储图中顶点信息;
一个二维数组(称为邻接矩阵)存储图中边或弧的信息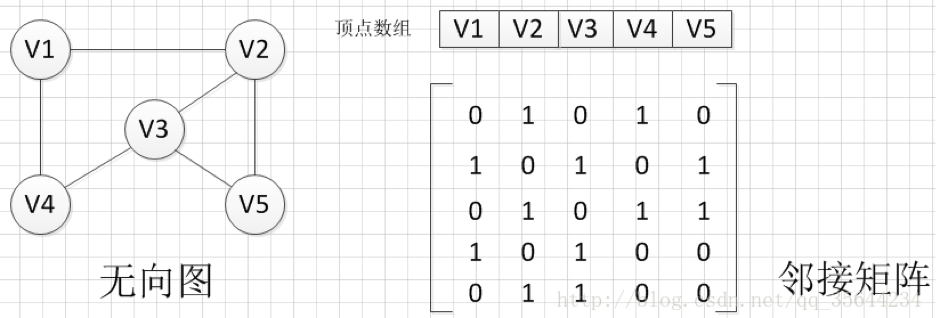
加权图使用权重代替1,∞表示不通
优点:
直观、容易理解,可以很容易的判断出任意两个顶点是否有边,最大的优点就是很容易计算出各个顶点的度。
缺点:
当需要表示完全图的时候,邻接矩阵是最好的表示方法,但是对于稀疏矩阵,由于它边少,但是顶点多,这样就会造成空间的浪费。
邻接表
邻接表是图的一种链式存储结构。主要是应对于邻接矩阵在顶点多边少的时候,浪费空间的问题。它的方法就是声明两个结构。
无向图示例: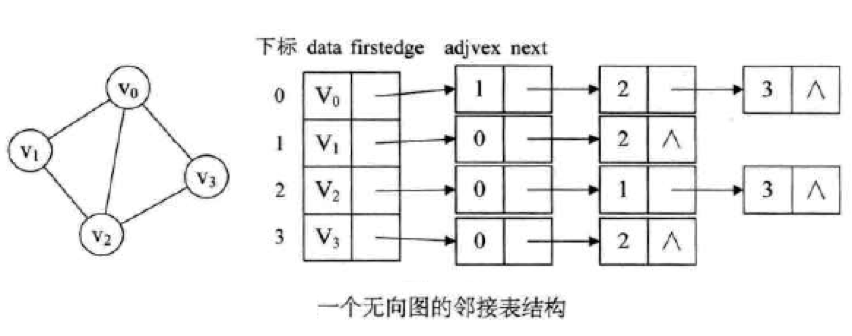
加权有向图示例: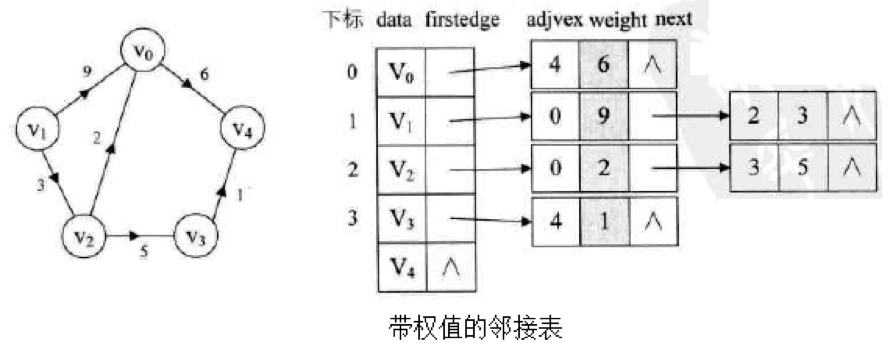
优点:
对于,稀疏图,邻接表比邻接矩阵更节约空间。
缺点:
不容易判断两个顶点是有关系(边),顶点的出度容易,但是求入度需要遍历整个邻接表。
十字链表
十字链表是有向图的一个专有的链表结构,我们之前也说了,邻接表对于我们计算顶点的入度是一个很麻烦的事情,而十字链表正好可以解决这个问题。十字链表和邻接表一样,他会有两个结构来表示图:其中一个结构用于保存顶点信息,另外一个结构是用于保存每条边的信息,如下图所示:
实线链接的链表表示出度,虚线表示入度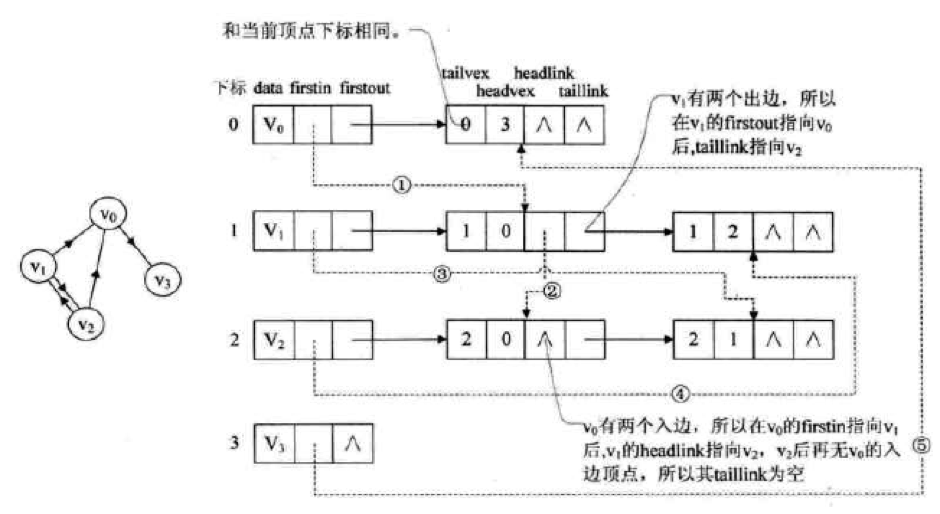
邻接多重表
邻接多重表是无向图的另一种链式存储结构。我们之前也说了使用邻接矩阵来存储图比价浪费空间,但是如果我们使用邻接表来存储图时,对于无向图又有一些不便的地方,例如我们需要对一条已经访问过的边进行删除或者标记等操作时,我们除了需要找到表示同一条边的两个结点。这会给我们的程序执行效率大打折扣,所以这个时候,邻接多重表就派上用场啦。
首先,邻接多重表同样是对邻接表的一个改进得到来的结构,它同样需要一个头结点保存每个顶点的信息和一个表结点,保存每条边的信息,他们的结构如下:
mark为标志域,例如标志是否已经访问过,ivex和jvex代表边的两个顶点在顶点表中的下标,ilink指向下一个依附在顶点ivex的边,jlink指向下一个依附在顶点jvex的边,weight 代表该边的权重。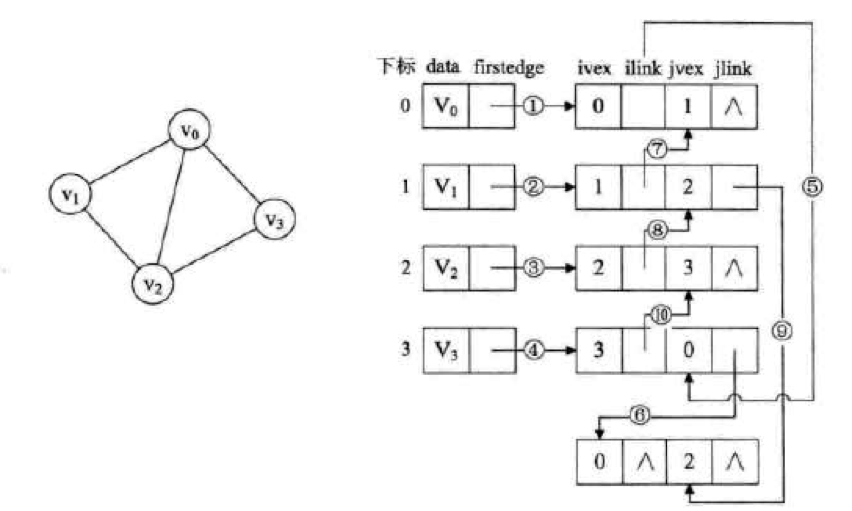
边集数组
边集数组是由两个一维数组构成,一个是存储顶点的信息,另一个是存储边的信息,这个边数组每个数据元素由一条边的起点下标(begin),终点下标(end)和权(weight)组成。带权图(网)的另一种存储结构是边集数组,它适用于一些以边为主的操作。用边集数组表示带权图时,列出每条边所依附的两个顶点及边上的权,即每个数组元素代表一条边的信息。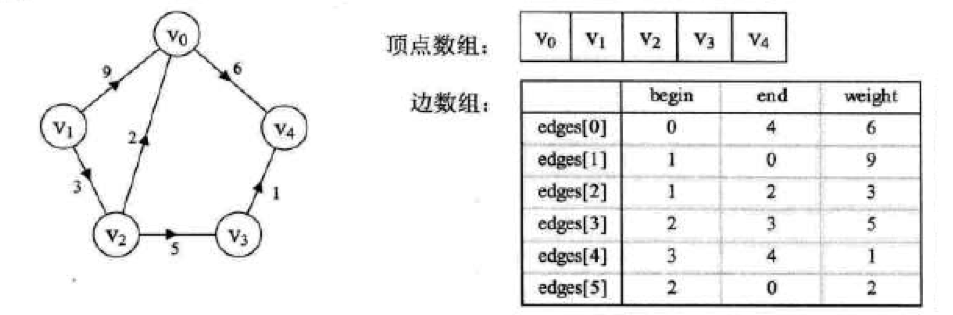
边集数组侧重于对边依次进行处理的操作,而不适合对顶点相关的操作。
图的遍历
图的遍历图和树的遍历类似,那就是从图中某一顶点出发访遍图中其余顶点,且使每一个顶点仅被访问一次,这个过程就叫做图的遍历。
对于图的遍历来说,如何避免因回路陷入死循环,就需要科学地设计遍历方案,通过有两种遍历次序方案:深度优先遍历和广度优先遍历。
深度优先遍历
深度优先遍历(Depth_First_Search),也称为深度优先搜索,简称DFS。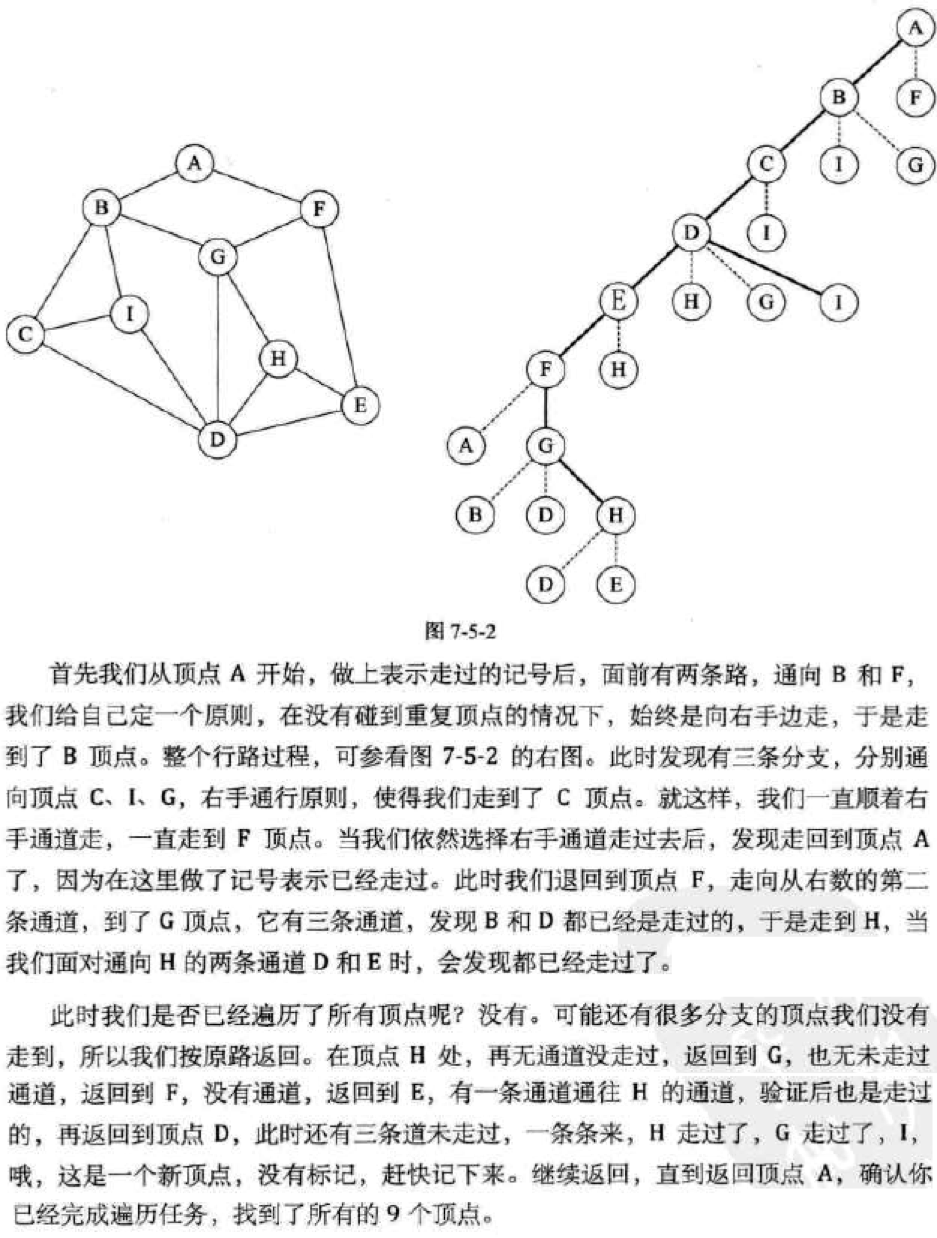
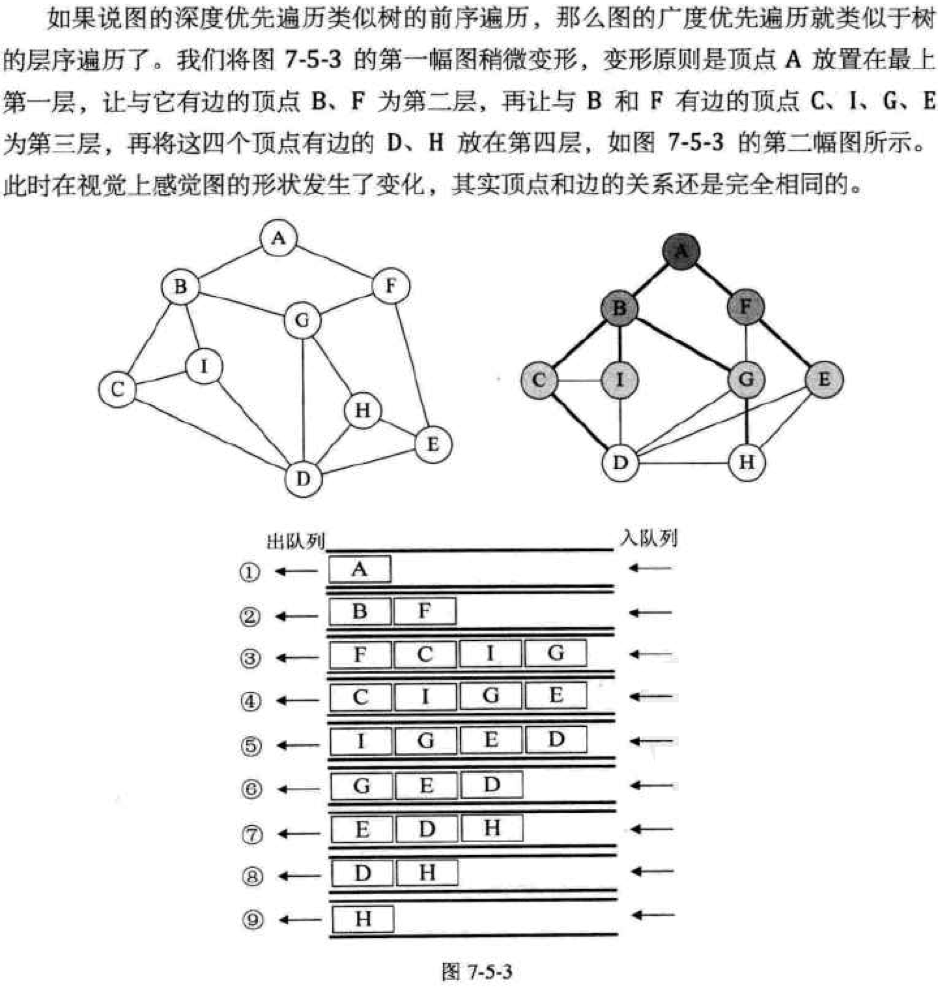
广度优先遍历
广度优先遍历(Breadth_First_Search),又称为广度优先搜索,简称BFS。
深度遍历类似树的前序遍历,广度优先遍历类似于树的层序遍历。