介绍一些常见的树,了解一些树的基本概念,具体代码操作不做详细说明。
二叉查找树
二叉排序树(Binary Sort Tree),又称二叉查找树(Binary Search Tree),亦称二叉搜索树。
二叉排序树或者是一棵空树,或者是具有下列性质的二叉树:
- 若左子树不空,则左子树上所有结点的值均小于或等于它的根结点的值;
- 若右子树不空,则右子树上所有结点的值均大于或等于它的根结点的值;
- 左、右子树也分别为二叉排序树。
查找:
若根结点的关键字值等于查找的关键字,成功。
否则,若小于根结点的关键字值,递归查左子树。若大于根结点的关键字值,递归查右子树。
若子树为空,查找不成功。
最差情况分析 O(n)
平均情况分析:O(logn)
插入:
首先执行查找算法,找出被插结点的父亲结点。判断被插结点是其父亲结点的左、右儿子。将被插结点作为叶子结点插入。
删除:
在二叉排序树删去一个结点,分三种情况讨论:
1) 若*p结点为叶子结点,即PL(左子树)和PR(右子树)均为空树。由于删去叶子结点不破坏整棵树的结构,则可以直接删除此子结点。
2) 若p结点只有左子树PL或右子树PR,此时只要令PL或PR直接成为其双亲结点f的左子树(当p是左子树)或右子树(当p是右子树)即可,作此修改也不破坏二叉排序树的特性。
3) 若p结点的左子树和右子树均不空。在删去p之后,为保持其它元素之间的相对位置不变,可按中序遍历保持有序进行调整,可以有两种做法:
其一是令p的左子树为f的左/右(依p是f的左子树还是右子树而定)子树,*s为p左子树的最右下的结点,而p的右子树为*s的右子树;
其二是令p的直接前驱(或直接后继)替代p,然后再从二叉排序树中删去它的直接前驱(或直接后继)-即让f的左子树(如果有的话)成为p左子树的最左下结点(如果有的话),再让f成为p的左右结点的父结点。
二叉堆 heap
在实际应用中,我们主要考虑最大堆(也称大顶堆)和最小堆(小顶堆)。其中最大堆(Max Heap)的根节点关键字(key)为所有节点关键字中最大值,且要求所有节点关键字的值大于等于其左孩子和右孩子的关键字。最小堆同理。
插入:新元素放在树最底层右边,然后上浮
删除根节点: 使用末节点替换根节点,然后对跟节点下沉。
删除任意节点:使用末节点替换被删除节点,然后对该节点先下沉再上浮。
堆的构建
方法1:插入法:
从空堆开始,依次插入每一个结点,直到所有的结点全部插入到堆为止。
时间:O(n*log(n))
方法2:调整法:
序列对应一个完全二叉树;从最后一个分支结点(n div 2)开始,到根(1)为止,依次对每个分支结点进行调整(下沉),
以便形成以每个分支结点为根的堆,当最后对树根结点进行调整后,整个树就变成了一个堆。
时间:O(n)
2-3查找树
一棵2-3查找树或为一颗空树,或由以下节点组成:
2-节点:含有一个键和两条链接,左链接指向的2-3树中的键都小于该节点,右链接指向的2-3树中的键都大于该节点。
3-节点:含有两个键和三条链接,左链接指向的2-3树中的键都小于该节点,中链接指向的2-3树中的键都位于该节点的两个键之间,右链接指向的2-3树中的键都大于该节点。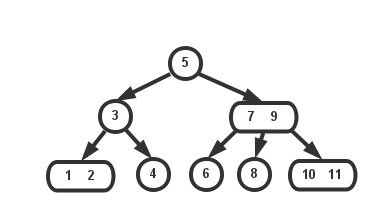
插入(难点)因为要维持平衡
每当有新的元素插入时,进行一次未命中查找,当有存放它的位置时,2-节点还尚有一个存储空间,它就存放。
如果遇到的是一个3-节点,没有位置放,则我们先把他变成一个4-节点,然后分情况讨论:
- 如果这个4-节点的父节点为2-节点,则将中键上提到父节点,形成2个3-节点
- 如果这个父节点也为3节点,则不断上提中键,直到遇到一个父节点为2-节点
- 如果一直到根节点全是3-节点,则分裂生成的4-节点为2个2-节点
红黑树
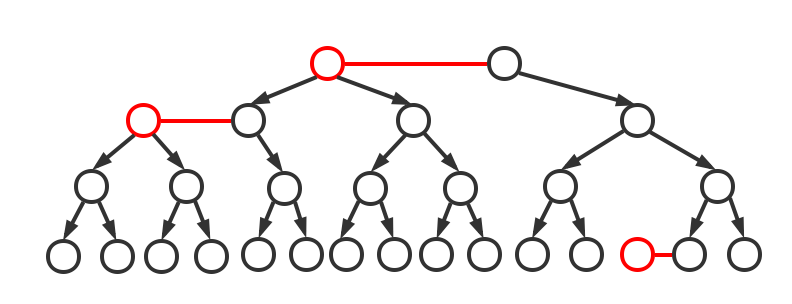
红黑树可以说利用二叉查找树对2-3查找树的实现,红链接将两个2-节点连起来构成一个3-节点,黑链接则是普通链接。这种实现的好处是可以使用二叉查找树高效的查找方法并能使用2-3树高校的平衡插入方法。事实上,将红黑树的红链接画平就是一个2-3树。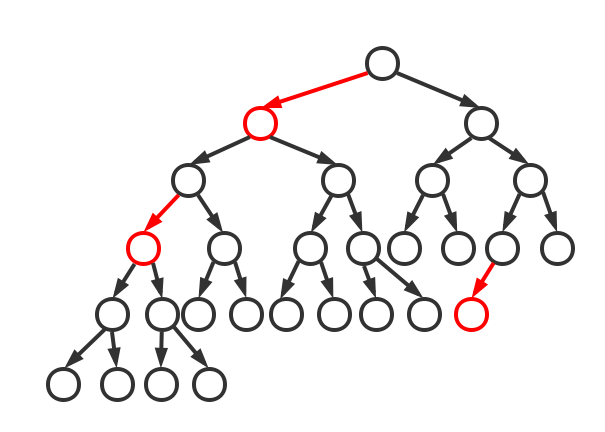
红黑树的性质:
- 节点是红色或黑色(红黑树结的的颜色实际上是指该节点与其父节点之间链接的颜色)
- 根节点是黑色 。根据节点颜色定义可得
- 所有叶子都是黑色(叶子是NIL节点)。
- 每个红色节点的两个子节点都是黑色。没有任何一个结点同时和两条红链接相连,不然就变成4-节点了.
- 该树是完美黑色平衡的,即任意空链接到根结点的路径上的黑链接数量相同。
- 红链接均为左链接。只允许红色左链接可以减少可能出现的情况,从而减少代码量。也有支持红色右链接的红黑树实现。
旋转:
左旋转将一个红色右链接转化为红色左链接,右旋转相反。网上分各种旋转的可能性,其实只需对比2-3树,把红链接链接的两个节点当作一个3节点来看就知道怎么旋转了。
插入:
可对比2-3树插入,结果再进行旋转保证红黑树性质即可。
删除(难点):结合具体情况具体分析。。。
AVL树
平衡二叉树又称AVL树,它或者是一棵空树,或者是具有下列性质的二叉树:它的左子树和右子树都是平衡二叉树,且左子树和右子树的深度之差的绝对值不超过1。
AVL树是最先发明的自平衡二叉查找树算法。在AVL中任何节点的两个儿子子树的高度最大差别为1,所以它也被称为高度平衡树,n个结点的AVL树最大深度约1.44log2n。
查找、插入和删除在平均和最坏情况下都是O(log n)。增加和删除可能需要通过一次或多次树旋转来重新平衡这个树。
平衡二叉树追求绝对平衡,条件比较苛刻,实现起来比较麻烦,每次插入新节点之后需要旋转的次数不能预知。
B树
一个 m 阶的B树满足以下条件:
- 树中每个结点最多含有m个孩子(m>=2);
- 除根结点和叶子结点外,其它每个结点至少有[ceil(m / 2)]个孩子;
- 若根结点不是叶子结点,则至少有2个孩子(特殊情况:没有孩子的根结点,即根结点为叶子结点,整棵树只有一个根节点);
- 所有叶子结点都出现在同一层。
每个非终端结点中包含有n个关键字信息: (n,P0,K1,P1,K2,P2,……,Kn,Pn)。其中:
a) Ki (i=1…n)为关键字,且关键字按顺序升序排序K(i-1)< Ki。
b) Pi为指向子树根的接点,且指针P(i-1)指向子树种所有结点的关键字均小于Ki,但都大于K(i-1)。
c) 关键字的个数n必须满足: [ceil(m / 2)-1]<= n <= m-1。
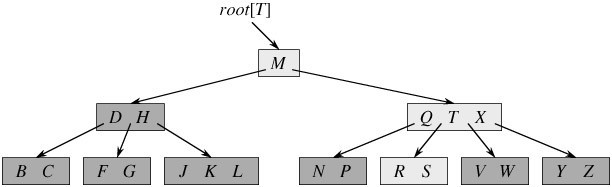
B树是对二叉查找树的改进。它的设计思想是,将相关数据尽量集中在一起,以便一次读取多个数据,减少硬盘操作次数。
B树为系统最优化大块数据的读和写操作。B树算法减少定位记录时所经历的中间过程,从而加快存取速度。普遍运用在数据库和文件系统。
假定一个节点可以容纳100个值,那么3层的B树可以容纳100万个数据,如果换成二叉查找树,则需要20层!假定操作系统一次读取一个节点,并且根节点保留在内存中,那么B树在100万个数据中查找目标值,只需要读取两次硬盘。
为什么计算机系统内会优先使用B树而不是红黑树?
计算机有一个局部性原理,就是说,当一个数据被用到时,其附近的数据也通常会马上被使用。所以当你用红黑树的时候,你一次只能得到一个键值的信息,而用B树,可以得到最多M-1个键值的信息。这样来说B树当然更好了。另外一方面,同样的数据,红黑树的阶数更大,B树更短,这样查找的时候当然B树更具有优势了,效率也就越高。
B+树
B+树是B树的变体,也是一种多路搜索树:
1.其定义基本与B树同,除了:
2.非叶子结点的子树指针与关键字个数相同;
3.非叶子结点的子树指针P[i],指向关键字值属于[K[i], K[i+1])的子树(B-树是开区间);
5.为所有叶子结点增加一个链指针;
6.所有关键字都在叶子结点出现;
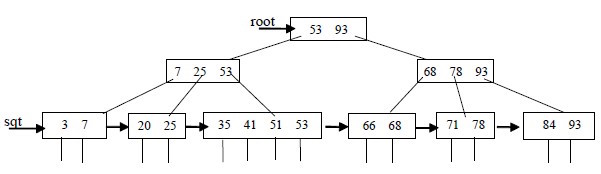
为什么说B+树比B 树更适合实际应用中操作系统的文件索引和数据库索引?
B+-tree的磁盘读写代价更低
B+-tree的内部结点并没有指向关键字具体信息的指针。因此其内部结点相对B 树更小。如果把所有同一内部结点的关键字存放在同一盘块中,那么盘块所能容纳的关键字数量也越多。一次性读入内存中的需要查找的关键字也就越多。相对来说IO读写次数也就降低了。B+-tree的查询效率更加稳定
由于非终结点并不是最终指向文件内容的结点,而只是叶子结点中关键字的索引。所以任何关键字的查找必须走一条从根结点到叶子结点的路。所有关键字查询的路径长度相同,导致每一个数据的查询效率相当。数据库索引采用B+树的主要原因是 B树在提高了磁盘IO性能的同时并没有解决元素遍历的效率低下的问题。正是为了解决这个问题,B+树应运而生。B+树只要遍历叶子节点就可以实现整棵树的遍历。而且在数据库中基于范围的查询是非常频繁的,而B树不支持这样的操作(或者说效率太低)。
注意了,没有B- 树。B-树就是B树,中间是横杠不是减号。
B*树
B-tree是B+-tree的变体,在B+树的基础上(所有的叶子结点中包含了全部关键字的信息,及指向含有这些关键字记录的指针),B树中非根和非叶子结点再增加指向兄弟的指针;B树定义了非叶子结点关键字个数至少为(2/3)\M,即块的最低使用率为2/3(代替B+树的1/2)。
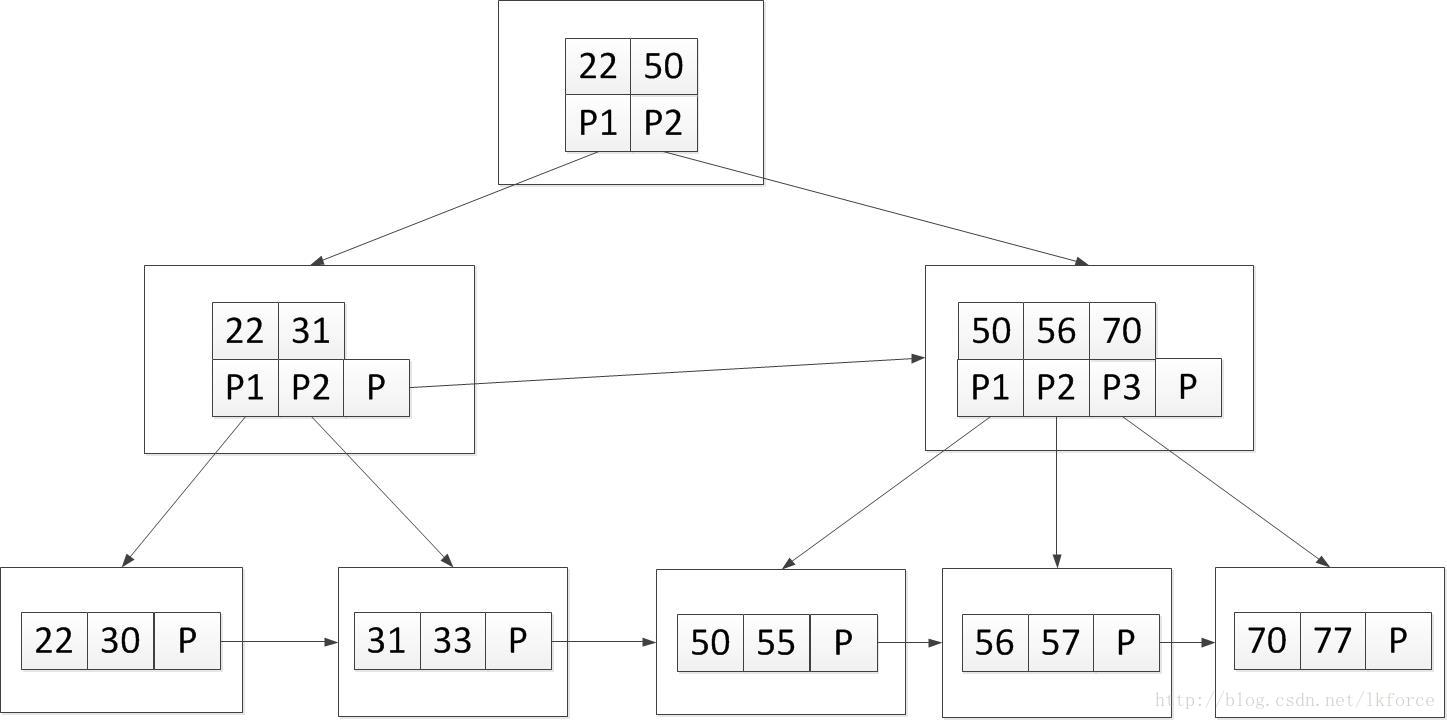
B+树的分裂:当一个结点满时,分配一个新的结点,并将原结点中1/2的数据复制到新结点,最后在父结点中增加新结点的指针;B+树的分裂只影响原结点和父结点,而不会影响兄弟结点,所以它不需要指向兄弟的指针。
B*树的分裂:当一个结点满时,如果它的下一个兄弟结点未满,那么将一部分数据移到兄弟结点中,再在原结点插入关键字,最后修改父结点中兄弟结点的关键字(因为兄弟结点的关键字范围改变了);如果兄弟也满了,则在原结点与兄弟结点之间增加新结点,并各复制1/3的数据到新结点,最后在父结点增加新结点的指针。
所以,B*树分配新结点的概率比B+树要低,空间使用率更高;
Trie树(字典树)
字典树又称单词查找树,Trie树,是一种树形结构,是一种哈希树的变种。典型应用是用于统计,排序和保存大量的字符串(但不仅限于字符串),所以经常被搜索引擎系统用于文本词频统计。它的优点是:利用字符串的公共前缀来减少查询时间,最大限度地减少无谓的字符串比较,查询效率比哈希表高。
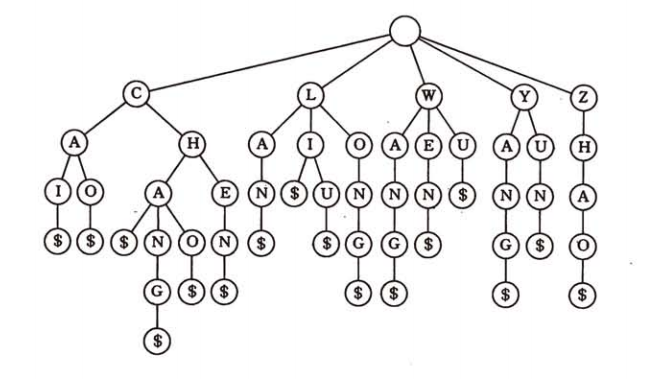
字典树很明显的就是用空间来换时间,空间复杂度特别大,比如字典数单单存26个小写字母,那么每个节点的孩子节点都有26个孩子节点,字典树中的每一层都保留着不同单词的相同字母。